Abstract
Synthetic time series generated by diffusion models enable sharing privacy-sensitive datasets, such as patients' functional MRI records. Key criteria for synthetic data include high data utility and traceability to verify the data source. Recent watermarking methods embed in homogeneous latent spaces, but state-of-the-art time series generators operate in data space, making latent-based watermarking incompatible. This creates the challenge of watermarking directly in data space while handling feature heterogeneity and temporal dependencies. We propose TimeWak, the first watermarking algorithm for multivariate time series diffusion models. To handle temporal dependence and spatial heterogeneity, TimeWak embeds a temporal chained-hashing watermark directly within the temporal-feature data space. The other unique feature is the ϵ-exact inversion, which addresses the non-uniform reconstruction error distribution across features from inverting the diffusion process to detect watermarks. We derive the error bound of inverting multivariate time series while preserving robust watermark detectability. We extensively evaluate TimeWak on its impact on synthetic data quality, watermark detectability, and robustness under various post-editing attacks, against five datasets and baselines of different temporal lengths. Our results show that TimeWak achieves improvements of 61.96% in context-FID score, and 8.44% in correlational scores against the strongest state-of-the-art baseline, while remaining consistently detectable.
Overview
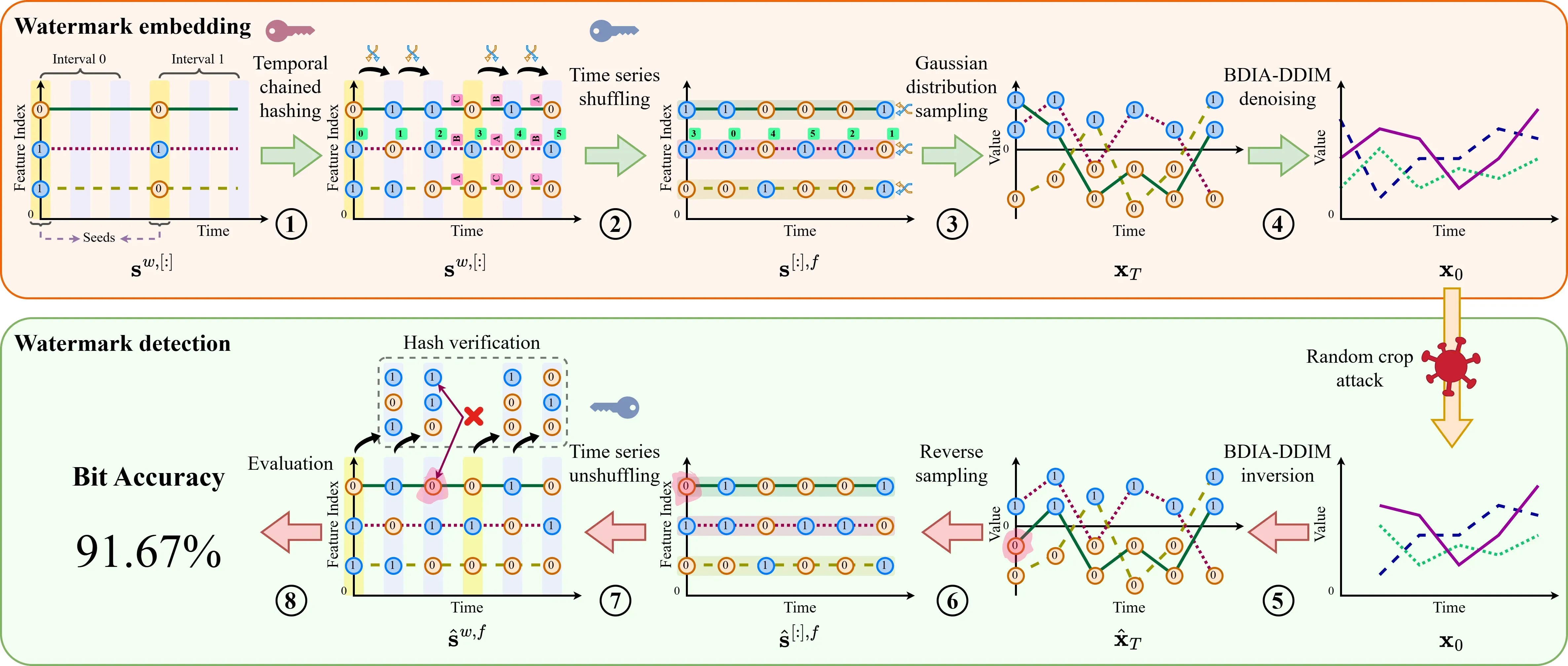
First, we assign random seeds at the beginning of each interval. 1 Temporally chained-hashing. A, B, and C (pink) show seeds being copied from the previous step and the feature order shuffled. 2 Shuffling the seeds for each series. Positional indices are highlighted in green. 3 Constructing an initial Gaussian noise. 4 Generating multivariate time series. 5 Reversing the diffusion process. 6 Recovering the watermark seed. 7 Unshuffling the seeds in the opposite way they were shuffled. 8 Bit accuracy between the hash and recovered seed.
Synthetic Data Quality and Watermark Detectability
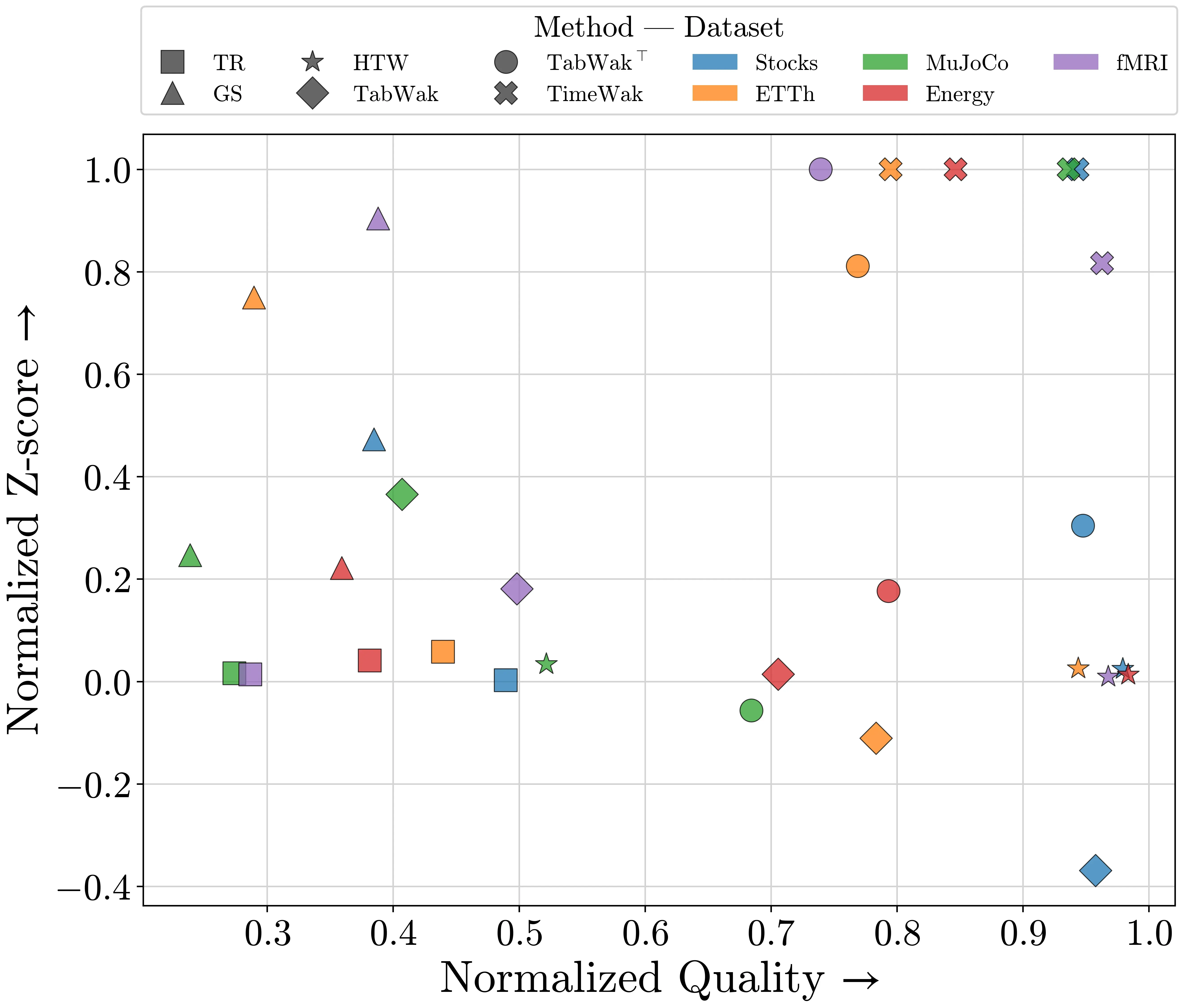
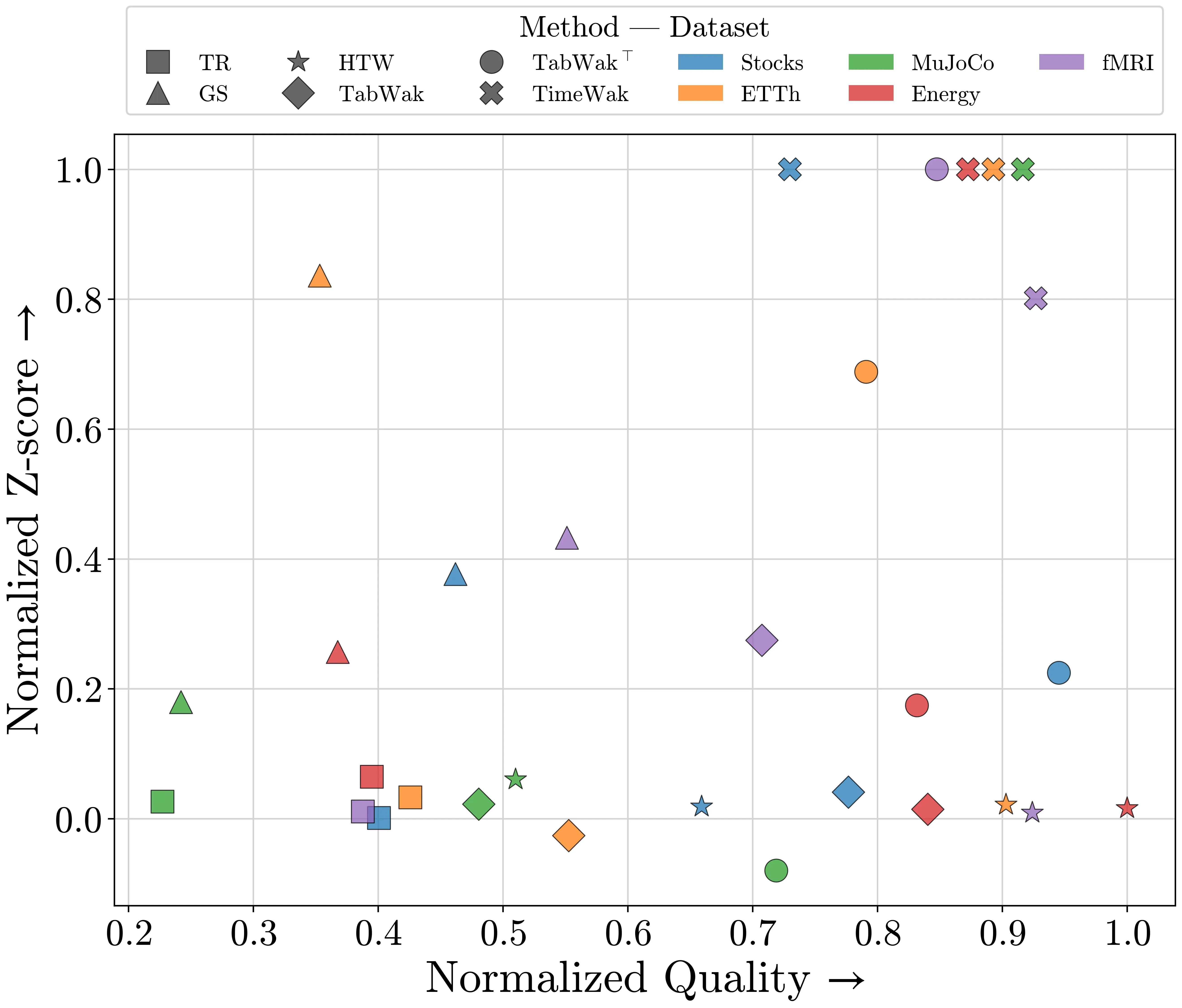
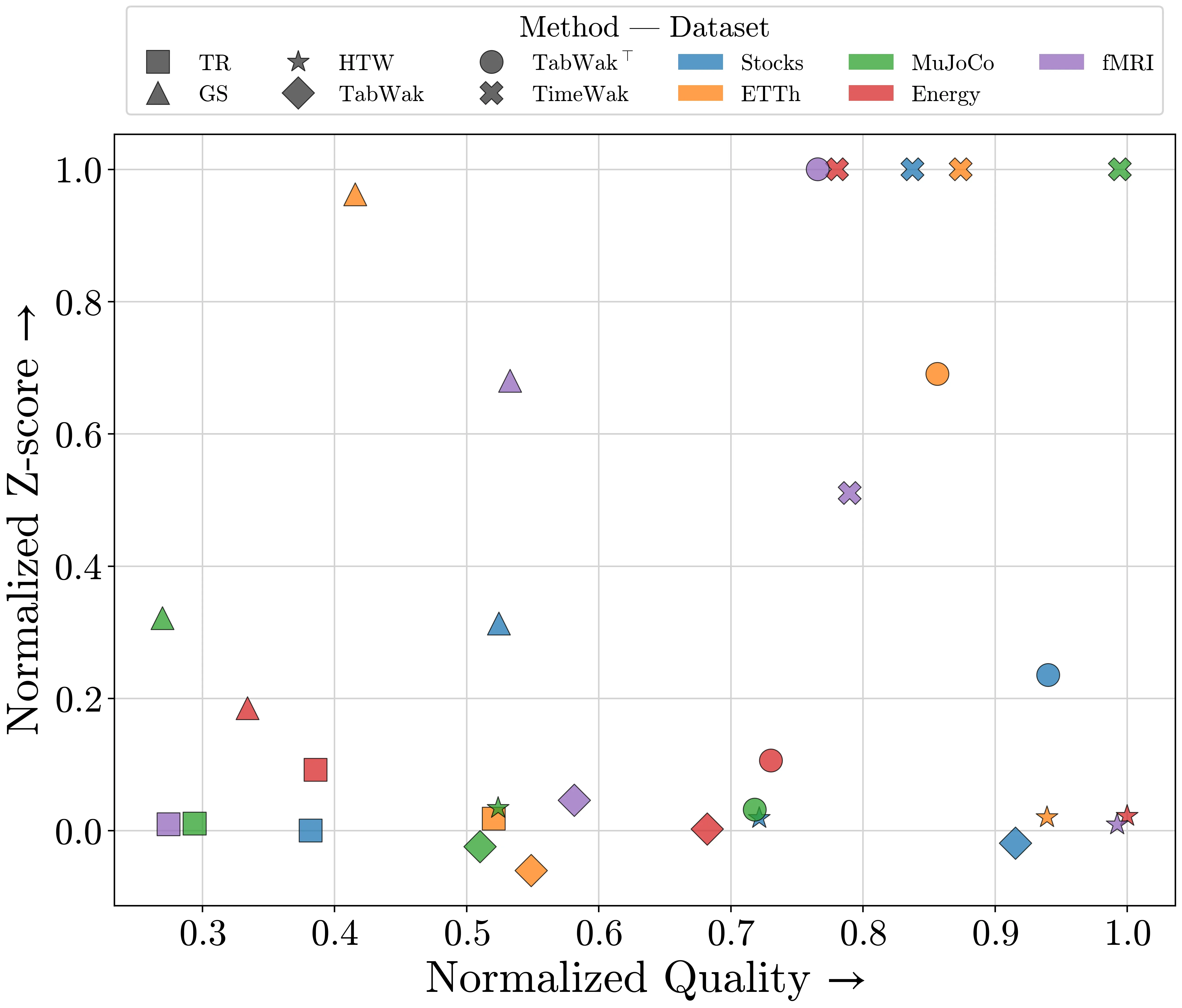
TimeWak consistently delivers top-tier performance across all metrics, outperforming or comparable to other baselines like HTW and TabWak⊤. Although HTW achieves higher-quality results, it fails to offer strong detectability, as reflected in its low Z-scores. In contrast, TimeWak and TabWak⊤ offer a far more favorable trade-off between quality and detectability.
TPR@0.1%FPR
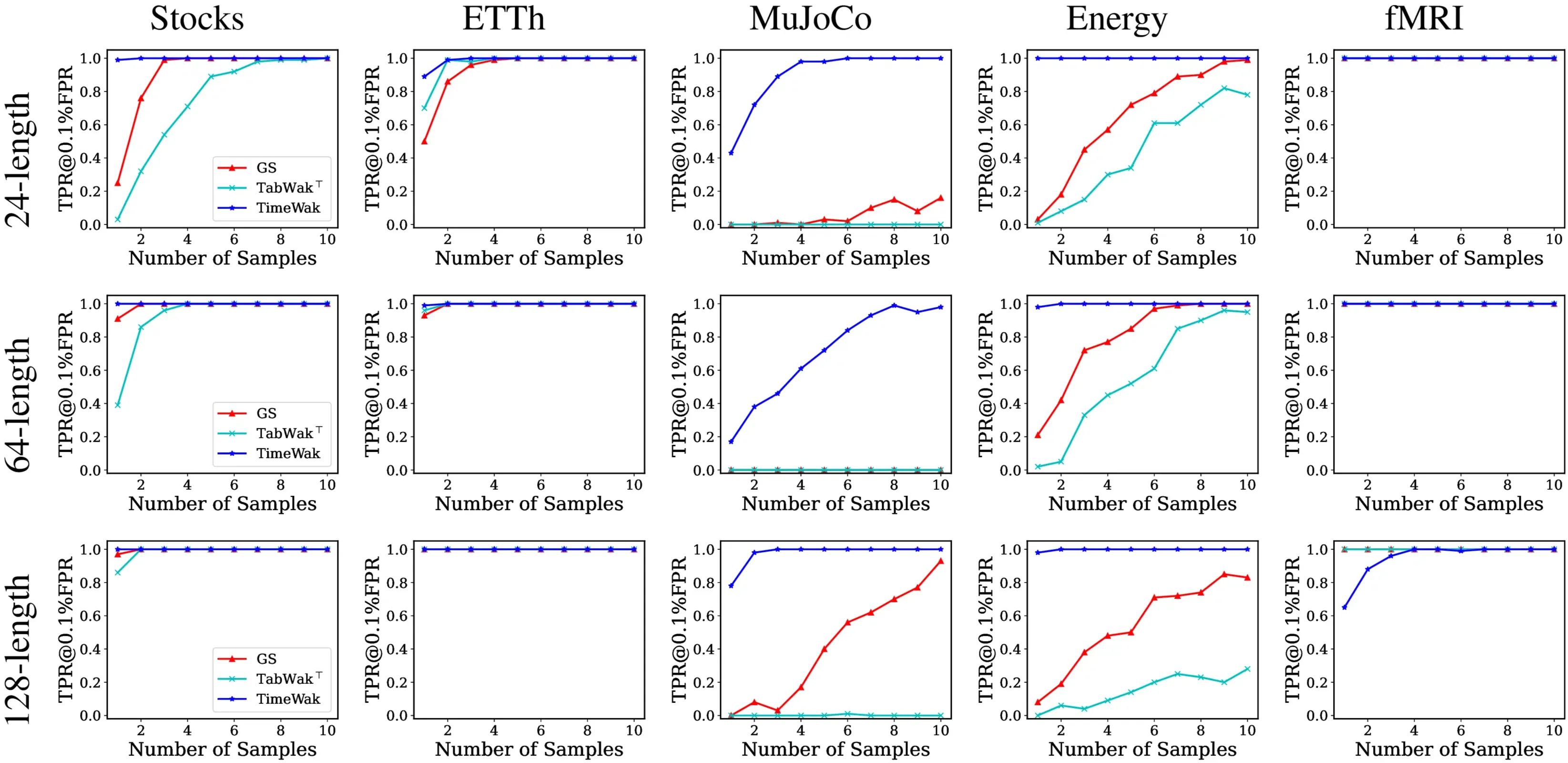
We present the TPR@0.1%FPR metric against the number of samples across five datasets under 24, 64 and 128 window sizes. In most cases, TimeWak consistently outperforms other baselines, such as Gaussian Shading and TabWak⊤, by achieving significantly higher TPR values. Notably, TimeWak reaches a perfect 1.0 TPR@0.1%FPR in the majority of scenarios, with 7 cases requiring only a single sample and 4 cases needing just 2 samples, demonstrating its strong detectability with minimal data requirements.
Robustness Against Post-Editing Attacks
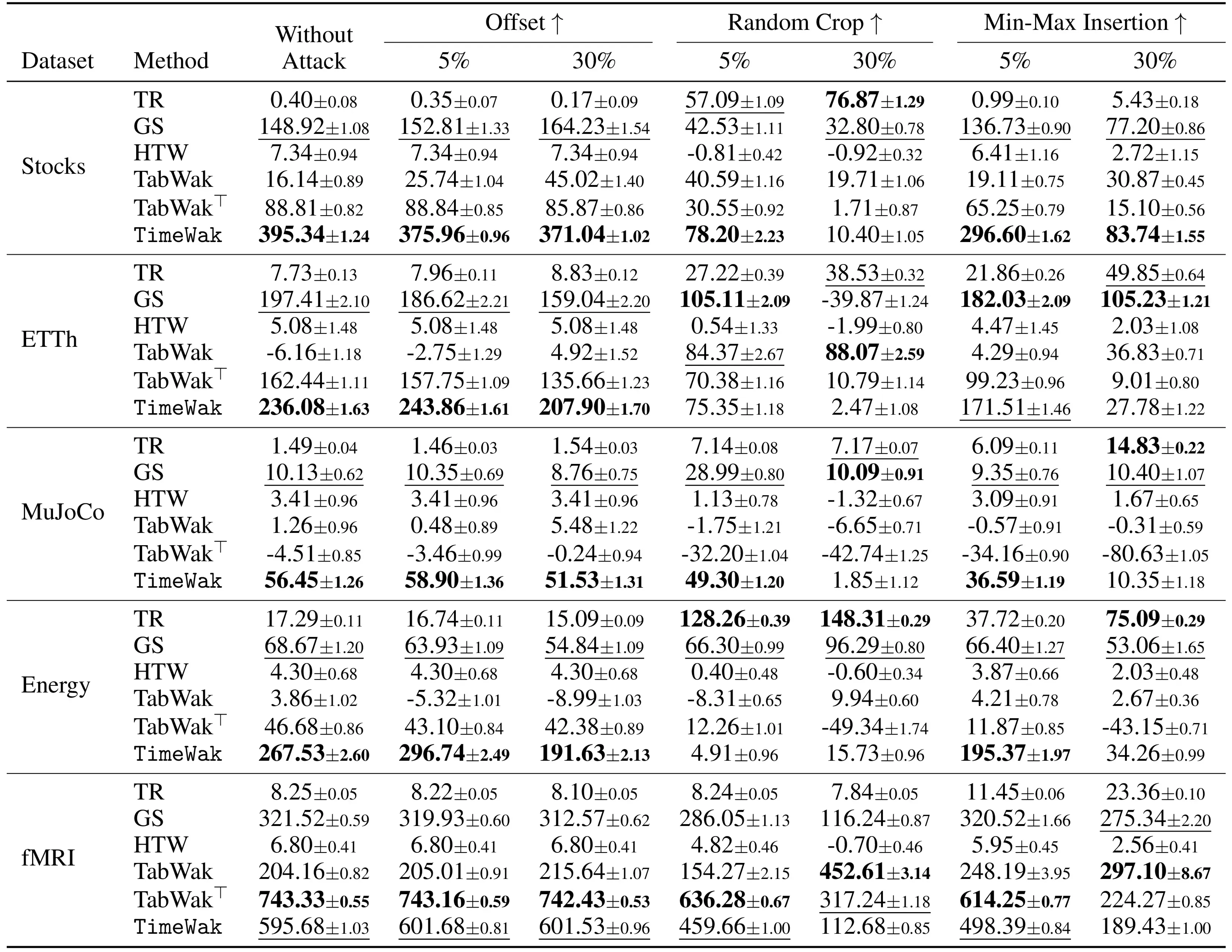
We present the Z-scores of 64-length watermarked synthetic time series data under three attacks, and averaged over 100 trials. Random cropping at 30% proves especially challenging, with several methods showing negative Z-scores. Nevertheless, TimeWak demonstrates the best overall robustness, consistently outperforming all baselines across most attack scenarios while maintaining high generation quality and accurate watermark detection.
Citation
@inproceedings{soi2025timewak, title = {TimeWak: Temporal Chained-Hashing Watermark for Time Series Data}, author = {Zhi Wen Soi and Chaoyi Zhu and Fouad Abiad and Aditya Shankar and Jeroen M. Galjaard and Huijuan Wang and Lydia Y. Chen}, booktitle = {NeurIPS}, year = {2025},}